English version below / Vai alla versione italiana
2. Can you give us a brief introduction to how the Austrian training and selection system for international competitions (and for EGMO in particular) works?
In Austria, the selection process for the EGMO, IMO (International Mathematical Olympiad) and MEMO (Middle European Mathematical Olympiad) consists of several competition rounds, starting with a preparatory course in the own school. In 2016/17, there were 68 such courses that were attended by a total of 862 students. This is followed by a course competition in March, where the the best 5 students from each course qualify for the regional competition.
The regional competition then takes place in April and consists of 4 problems to be solved within 4 hours. It is held concurrently in 3 locations in Austria with around 40 to 60 students participating in each location.
The best 40 students at the regional competitions (around 14 from each of the three locations) are invited to a 10 day training camp in April/May, which concludes with a preliminary national competition with 4 problems in 4.5 hours, reducing from 40 to 24 students. The remaining 24 students are again invited for a 10 day training camp, directly followed by the national competition in May, which consists of two competition days of 4.5 hours and 3 problems each.
The 6 best Austrian students will then be sent to IMO, while places 7 to 12 qualify for the MEMO. In addition, in 2018 we will send the best 4 girls from the national competition 2017 to the EGMO.
Additionally, there does exist a track for beginners. Students who participate in the Mathematical Olympiad for the first time (and satisfy some additional conditions like a maximum age) may, instead of the regional competition, participate in the beginner's regional competition, which however does not lead up to any national or international competitions.
3. How severe do you believe the “gender gap” in maths competition in your country to be, in particular compared to other European countries? More specifically, did you feel any sort of “obstacles” to overcome in your past as a contestant for being a woman?
I personally would prefer to believe that such a gender gap does not exist. That is, I have never personally experienced anyone trying to prevent me from being successful or to dissuade me from taking part in maths competitions.
This being said, I cannot deny that there do seem to exist differences in role models that appear to encourage boys more than girls to go into a mathematical career. We seem to lose especially many girls from our maths olympiad preparation courses at the age of around 14 years. Based on anecdotal evidence, at this age some girls in our courses are told by their parents, and to a lesser extent by their teachers, things like "In mathematics you are good anyway and don't need extra training; Why don't you focus more on the other subjects where your grades are not that good?" or "Mathematics is fine, but for your future career you will need languages more.". This is a phenomenon that seems to affect boys less often.
It would appear to me that for boys it is more socially acceptable to excel at soccer but suck at maths, or to excel at maths but suck at handicrafts, or to excel at handicrafts but suck at soccer, whereas girls are often expected to be at least adequate in every subject, but not so much to strive for excellence in any single one of them. Consequently, it might be that when they find that they are good at maths, or any other field for that matter, at least some of them will consider themselves lucky for not having to invest much effort into getting good grades there, and will go and put that extra time into areas where they feel they are lacking. From a Mathematical Olympiad point of view, this of course means that we do miss out on a lot of potential talent.
This personal hypothesis of mine seems to be supported by statistical data from the Mathematical Kangaroo competition in Austria (an annual, international, 30 question, multiple-choice math quiz that many schools and more than 100 000 students in Austria take part in each year): While the average scores of boys and girls are fairly similar -- girls score "only" around 3.5% lower than boys during the 9 years of compulsory school attendance --, the standard deviation of girls is lower compared to that of the boys already in the first year of school, and progressively grows even smaller with each consecutive year. That is, with each year there are more girls close to the average score and fewer outliers in either direction. To give an example of what such a distribution typically looks like in the higher grades, here we can see the distribution in grade 10 of the year 2016:
Fig. 1: Mathematical Kangaroo scores of grade 10 in the competition 2016
Interestingly, we find the same data also in entirely different fields: The PISA study 2012, which covers the fields mathematics, reading and science, finds that while Austrian girls do better than boys in reading, worse in mathematics and around equally in science, again in all three fields they have lower standard deviations than boys, meaning that more of them have average values and fewer of them have exceptionally good or bad results:
Fig. 2a: PISA 2012 results of Austria in field Mathematics
Fig. 2b: PISA 2012 results of Austria in field Reading
Fig. 2c: PISA 2012 results of Austria in field Science
Certainly, this is only one out of many potential aspects that might contribute to Austria sending IMO teams that on average had only 8.3% girls in the past 30 years. Neither can I give a comprehensive list of all contributing factors, especially not within the bounds of a blog article such as this, nor am I aware of any ongoing scientific efforts to study this phenomenon. But out of the many aspects involved when it comes to girls and mathematics, this is one that appeared worth discussing to me.
As far as a comparison to the situation in other European countries is concerned, as I have lived abroad only for a small portion of my life, I would not dare to venture any guesses here.
4. Do you believe this gap mirrors a similar situation in schools or higher education?
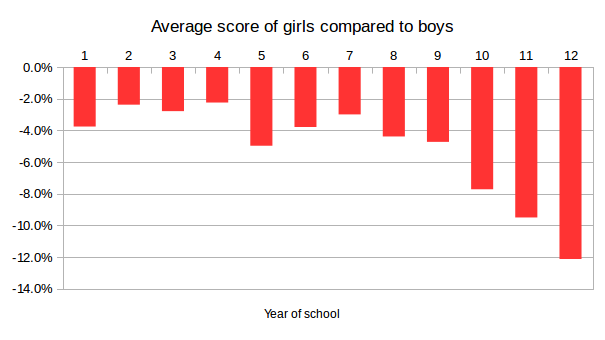
I mentioned above that up to the end of compulsory school attendance (which is 9 years in Austria), the Mathematical Kangaroo scores of boys and girls are similar within 3.5%. This changes drastically in the later years of school though, where average point score differences increase to up to 12%:
Fig. 3: Mathematical Kangaroo scores of girls compared to boys
My personal assumption is that at that age, many boys decide to go into technical colleges (which are a type of high quality secondary education that many countries envy Austria for) or secondary schools with a more scientific focus, whereas girls more often go into secondary schools with a focus on languages, tourism, trade or arts (and as a result of this choice get less mathematical training before they participate in the competition, which reflects in the scores).
As far as my observations go, neither of these school types discriminates against any gender, and will happily accept qualified students in whatever shape they come -- with some of these schools going out of their way to especially invite typically underrepresented minorities. So by and large, the selection of a school type appears to be a free choice that each student takes individually based on their interests.
It is of course surprising then that in spite of very similar levels of knowledge -- remind you that the PISA study quoted above found virtually no difference in scientific knowledge between boys and girls at age 15 --, so many more boys than girls decide to go into STEM fields.
I think this powerfully demonstrates the power that role models, societal expectations, and fear of discrimination (without much evidence that this discrimination actually takes place), can have on our seemingly free choices -- and as such is certainly a very challenging social issue to tackle.
5. What influence do you think EGMO has on the perception of women in mathematics?
I think it is a double-edged sword: On the one hand, it helps to strengthen the public image of women as capable of achieving excellence in mathematics, and it also gives young girls, who might be afraid of competing directly with boys, the chance to meet in a group of equals and to test their strength.
On the other hand, I do fear that it also perpetuates the image of women needing special support to succeed in technical fields, which I personally think is not at all the case.
Versione italiana a seguire / Back to English
2. Ci puoi raccontare brevemente come funzionano allenamento e selezione per le competizioni internazionali (e per le EGMO in particolare) in Austria?
In Austria la selezione per le EGMO, le IMO e le MEMO avviene mediante vari livelli di gare, iniziando con un corso di preparazione nelle singole scuole. Nel 2016/17 ci sono stati 68 di questi corsi, cui hanno preso parte complessivamente 862 studenti. A conclusione dei corsi c’è stata una gara, nel mese di marzo, nella quale i cinque migliori studenti di ogni corso si qualificano per la gara regionale.
La gara regionale è in aprile ed è costituita da quattro problemi da risolvere in quattro ore. Si tiene in contemporanea in tre sedi in Austria, in ciascuna delle quali sono presenti tra i 40 e i 60 studenti.
I migliori 40 studenti alle gare regionali (all’incirca 14 da ciascuna sede) vengono invitati ad uno stage di 10 giorni ad aprile/maggio, al termine del quale c’è una prima gara nazionale di quattro problemi in 4 ore e mezza, che seleziona 24 dei 40 partecipanti. Questi 24 sono invitati per un altro stage di 10 giorni, seguito immediatamente dalla gara nazionale a maggio, che si svolge su due giorni, con 3 problemi in 4 ore e mezza ciascuno.
I migliori 6 studenti austriaci partecipano alle IMO, mentre coloro che si classificano tra il settimo e il dodicesimo posto inclusi vanno alle MEMO. Inoltre nel 2018 manderemo le migliori 4 ragazze della gara nazionale 2017 alle EGMO.
Oltre a questo, esiste un programma per principianti. Gli studenti che partecipano alle Olimpiadi di Matematica per la prima volta (e soddisfano certi vincoli, ad esempio di età massima) possono partecipare, invece che alla gara regionale, alla gara regionale per principianti, che tuttavia non dà sbocco ad alcuna ulteriore gara nazionale o internazionale.
3. Quanto pensi sia marcata la disuguaglianza di genere nelle gare di matematica in Austria, in particolare rispetto alle altre nazioni europee? Più nello specifico hai mai avuto l’impressione di dover superare degli “ostacoli” in quanto donna nel tuo passato da concorrente?
Personalmente mi piacerebbe credere che questa disuguaglianza di genere non esista. Nello specifico: io non ho mai avuto esperienza personale di qualcuno che tentasse di impedirmi di aver successo o prender parte alle gare di matematica.
Premesso ciò, non posso negare che sembra proprio che ci siano differenze nelle figure di riferimento che apparentemente incoraggiano più ragazzi che ragazze alla carriera matematica. Perdiamo un gran numero di ragazze attorno ai 14 anni nei nostri corsi di preparazione alle Olimpiadi di Matematica. Basandomi su aneddoti, più o meno a quell’età alcune ragazze nei nostri corsi si sentono dire dai propri genitori e, in misura minore, dai propri insegnanti cose come “In matematica sei brava comunque, non hai bisogno di ulteriore preparazione. Perché non ti concentri un po’ di più sulle altre materie, in cui i tuoi voti non sono così buoni?” o “La matematica non è male, ma nella tua carriera avrai più bisogno di conoscere le lingue.” Questo fenomeno sembra essere meno rilevante per i maschi.
Mi sembra che per i ragazzi sia più accettabile essere bravi a giocare a calcio e scarsi in matematica, o essere bravi in matematica e scarsi nelle attività pratiche, o essere bravi nelle attività pratiche e scarsi a calcio, mentre dalle ragazze ci si aspetta che siano come minimo sufficienti in ogni materia, ma non necessariamente che puntino all’eccellenza in alcuna di esse. Di conseguenza è possibile che quando si rendono conto di essere brave in matematica, o in un qualunque altro ambito, almeno una parte di loro si senta fortunata di non doversi sforzare più di tanto per avere buoni voti in quella materia e concentri il proprio impegno in altre aree in cui senta di essere più in difficoltà. Dal punto di vista delle Olimpiadi di Matematica questo significa che molto talento potenziale va perduto.
Questa mia ipotesi personale sembra essere supportata anche da dati statistici tratti dal Kangourou della Matematica in Austria (una gara internazionale di 30 domande a risposta multipla cui in Austria partecipano molte scuole e più di 100 000 studenti ogni anno): sebbene i punteggi medi di ragazze e ragazzi siano abbastanza simili – le ragazze hanno un punteggio medio “solo” del 3.5% inferiore a quello dei ragazzi nei 9 anni della scuola dell’obbligo –, la deviazione standard delle ragazze è più bassa rispetto a quella dei ragazzi già dal primo anno di scuola e diventa sempre minore man mano che si sale di anno. Ogni anno, quindi, ci sono più ragazze vicine al punteggio medio e meno eccezioni in entrambe le direzioni. Per avere un esempio di come appare una distribuzione del genere nelle classi superiori, possiamo vedere in questa immagine la distribuzione per i quindicenni (decima classe nel sistema austriaco, seconda superiore nel sistema italiano) nel 2016:
Fig. 1: Punteggi per la decima classe al Kangourou della Matematica nella gara 2016
È abbastanza interessante che gli stessi dati saltino fuori anche in campi completamente diversi: lo studio PISA 2012, che copre matematica, lettura e scienze, mostra che se da un lato le ragazze austriache hanno punteggi più alti dei ragazzi nella lettura, più bassi in matematica e sostanzialmente uguali in scienze, dall’altro in tutte e tre le discipline hanno una deviazione standard più bassa rispetto ai ragazzi, cioè la maggior parte di loro ha punteggi medi e solo una piccola parte ha risultati particolarmente buoni o cattivi:
Fig. 2a: Risultati PISA 2012 per l’Austria nel settore Matematica
Fig. 2b: Risultati PISA 2012 per l’Austria nel settore Lettura
Fig. 2c: Risultati PISA 2012 per l’Austria nel settore Scienze
Chiaramente questo è solo uno dei tanti possibili motivi che hanno contribuito al fatto che negli ultimi trent’anni l’Austria mandasse alle IMO delle squadre in cui le ragazze in media sono state solo l’8.3%. Non posso certo pensare di fornire una lista esaustiva di tutti i fattori che hanno avuto parte in questo, in particolar modo non nei limiti di un articolo come questo, né sono al corrente di alcuno studio scientifico in merito. Ma di tutti i vari aspetti che entrano in gioco quando si parla di ragazze e matematica, mi è sembrato che questo meritasse una discussione.
Per quanto riguarda i paragoni con le altre nazioni europee, avendo vissuto all’estero solo per un breve periodo della mia vita, non oso fare alcuna speculazione in merito.
4. Ritieni che questa disuguaglianza rifletta una situazione simile nelle scuole e nell’istruzione universitaria?
Come ho detto nella risposta precedente, fino alla fine della scuola dell’obbligo (che in Austria è di 9 anni), i punteggi di ragazzi e ragazze ai Kangourou della Matematica differiscono meno del 3.5%. Questo però cambia drasticamente negli anni successivi, con un aumento della differenza tra i punteggi medi fino al 12%:
Fig. 3: Punteggi ai Kangourou della Matematica: differenza tra ragazze e ragazzi
La mia impressione è che a quell’età molti ragazzi decidono di andare alle scuole tecniche (un tipo di scuola secondaria superiore di alto livello che molte nazioni invidiano all’Austria) o a scuole secondarie superiori con una maggiore attenzione alle materie scientifiche, mentre le ragazze scelgono scuole secondarie più orientate alle lingue, al turismo, al commercio o alle arti (e di conseguenza hanno meno ore di matematica alle spalle quando affrontano le gare, cosa che si ripercuote sui punteggi).
Personalmente credo che nessun tipo di scuola discrimini in base al genere e che tutte accettino studenti preparati, indipendentemente da ogni altro aspetto – addirittura alcune scuole si sforzano notevolmente per attirare studenti da minoranze sottorappresentate. Mi sento di dire che la scelta della scuola è una scelta personale, che ogni studente fa in base ai propri interessi.
È però sorprendente che nonostante i livelli di preparazione molto simili – come dicevo sopra, lo studio PISA non mostra alcuna differenza sostanziale nelle conoscenze scientifiche tra ragazze e ragazzi di 15 anni – ci siano molti più ragazzi che ragazze nelle discipline STEM.
Credo che questo mostri molto bene l’impatto che le figure di riferimento, le aspettative della società e la paura della discriminazione (senza molti indizi del fatto che questa discriminazione avvenga effettivamente), possono avere sul nostro (apparentemente) libero arbitrio – questa è una questione sociale molto difficile da affrontare.
5. Che effetto pensi che abbiano le EGMO sulla visione delle donne nella matematica?
Penso sia un’arma a doppio taglio: da un lato aiuta a rinforzare nel pubblico l’idea che le donne possano raggiungere l’eccellenza in matematica e dà inoltre alle ragazze più giovani, che potrebbero essere restie a confrontarsi direttamente con i maschi, la possibilità di incontrarsi in un gruppo di pari e mettere alla prova le proprie capacità.
D’altro canto, ho paura che ribadisca l’idea che le donne abbiano bisogno di un aiuto speciale per aver successo in ambito tecnico-scientifico, cosa che personalmente ritengo del tutto falsa.